Unit 1
Collaborative discussion post
Refer to the article by Padhy et al. (2021), specifically Table 1, where the authors present a list of factors which they consider influence the reusability of a piece of object-oriented software.
In this collaborative discussion, you are required to prioritise this list, presenting your argument for the priorities assigned.
Quantifying software reusability: What actually matters?
Over the course of the history of computer science, various frameworks have been developed for evaluating algorithm and software complexity and reusability. Padhy, Panigrahi and Neeraja (2021) discuss metrics such as fan-in, fan-out, cyclomatic complexity (CC), ‘Metrics for Object Oriented Design’ (MOOD), and Chidamber & Kemerer metrics suite (CK metrics). The metrics can help optimize a software solution but must be understood and appropriately prioritized.
Cyclomatic complexity described by McCabe (1976) measures the numbers of execution paths in application. Similarly, fan-in and fan-out defined by Henry and Kafura (1981) track information flow. These metrics are perhaps the most valuable, allowing to predict how difficult it is to design and test software or reuse a certain algorithm for a different purpose.
For object-oriented development, in addition to measuring the effectiveness of the execution and information flow, it makes sense to quantify and measure the proper application of this development paradigm, which CK and MOOD try to do.
MOOD’s coupling factor (COF) and CK’s coupling between object classes (CBO) show how interdependent different classes are and hint at the possibility that multiple classes share the same responsibility and refactoring is due. Similarly, CK’s lack of cohesion in methods (LCOM) reveals whether class’ methods access the same fields. Low cohesion indicates that the class may need to be split or methods made static, increasing the classes’ independence and their reusability.
MOOD’s clustering factor shows if classes form independent clusters that can be reused without bringing unnecessary dependencies. This ensures modularity of a solution, where each module takes on a specific set of responsibilities, can be worked on separately, or even redistributed in a form of a library.
Other metrics in the MOOD and CK frameworks focus heavily on the application of OOP’s paradigms, but these aspects should be applied contextually. For instance, CK’s depth of inheritance tree and number of children show how likely changes to a single class will affect the application. However, it may be unwise to limit inheritance for the sake of meeting the metric requirement. Instead, these aspects must be addressed in the application’s architecture design to ensure both its proper function and the ease of its later support.
Prioritizing the metrics, I propose the following order:
- Cyclomatic complexity, fan-in, and fan-out that describe how easy it is to properly design, test, and support an algorithm;
- Coupling factor (COF, CBO) and lack of methods cohesion (LCOM) that enforce proper design of classes;
- Clustering factor to ensure modularity of the solution.
Finally, the use of any metrics should be a guiding but not a defining force in software development. Metrics can aid in locating the areas for improvement in solution’s codebase, but rigidly optimizing for metrics can instead be detrimental to the development process, shifting the development team’s focus from delivering a functional solution.
References
Henry, S. and Kafura, D. (1981) ‘Software Structure Metrics Based on Information Flow’, IEEE Transactions on Software Engineering, SE-7(5), pp. 510–518. Available at: https://doi.org/10.1109/TSE.1981.231113.
McCabe, T.J. (1976) ‘A Complexity Measure’, IEEE Transactions on Software Engineering, SE-2(4), pp. 308–320. Available at: https://doi.org/10.1109/TSE.1976.233837.
Padhy, N., Panigrahi, R. and Neeraja, K. (2021) ‘Threshold estimation from software metrics by using evolutionary techniques and its proposed algorithms, models’, Evolutionary Intelligence, 14(2), pp. 315–329. Available at: https://doi.org/10.1007/s12065-019-00201-0.
ePortfolio activities
‘Think Python’ is an introduction to Python programming for beginners. It starts with basic concepts of programming and is carefully designed to define all terms when they are first used and to develop each new concept in a logical progression. Larger pieces, like recursion and object-oriented programming, are divided into a sequence of smaller steps and introduced over the course of several chapters.
You are able to access the GitHub repo of 'Think Python', or you can use the original source from Green Tea Press.
Take a look at chapter 15 of 'Think Python', from page 147. Also, take a look at 'point.py' from GitHub. Work through the guidance and experiment with the code in PyCharm.
Upon evaluating the source code from the book, I first decided to optimize it and incorporate the point- and shape-related logic in the classes’ definitions. This allowed to reuse the logic later to complete the tasks. The application of the object-oriented approach allows to associate the values and operations with their respective objects, thus making code navigation and management easier.
Exercise 15.1
Write a definition for a class named Circle with attributes center and radius, where center is a Point object and radius is a number.
Instantiate a Circle object that represents a circle with its center at (150, 100) and radius 75.
Write a function named point_in_circle that takes a Circle and a Point and returns True if the Point lies in or on the boundary of the circle.
Write a function named rect_in_circle that takes a Circle and a Rectangle and returns True if the Rectangle lies entirely in or on the boundary of the circle.
Write a function named rect_circle_overlap that takes a Circle and a Rectangle and returns True if any of the corners of the Rectangle fall inside the Circle. Or as a more challenging version, return True if any part of the Rectangle falls inside the Circle.
class Point:
"""
Represents a point in a 2D space.
:ivar x: The x-coordinate of the point.
:type x: float
:ivar y: The y-coordinate of the point.
:type y: float
"""
def __init__(self, x, y):
self.x = x
self.y = y
def __str__(self):
return f"({self.x}, {self.y})"
def distance_to(self, other_point):
"""
Calculate the distance between this point and another point.
:param other_point: The other point to calculate distance to.
:type other_point: Point
:return: The distance between the two points.
:rtype: float
"""
import math
return math.sqrt((self.x - other_point.x) ** 2 + (self.y - other_point.y) ** 2)
class Rectangle:
"""
Represents a rectangle in a 2D space.
:ivar width: The width of the rectangle.
:type width: float
:ivar height: The height of the rectangle.
:type height: float
:ivar corner: The bottom-left corner of the rectangle as a Point object.
:type corner: Point
"""
def __init__(self, width, height, corner):
self.width = width
self.height = height
self.corner = corner
def get_points(self):
"""
Returns all four corner points of the rectangle.
:return: A tuple containing the bottom-left, bottom-right, top-left, and top-right points.
:rtype: tuple(Point, Point, Point, Point)
"""
bottom_left = self.corner
bottom_right = Point(self.corner.x + self.width, self.corner.y)
top_left = Point(self.corner.x, self.corner.y + self.height)
top_right = Point(self.corner.x + self.width, self.corner.y + self.height)
return bottom_left, bottom_right, top_left, top_right
def find_center(self):
"""Returns a Point at the center of the Rectangle.
returns: new Point
"""
center_x = self.corner.x + self.width / 2.0
center_y = self.corner.y + self.height / 2.0
return Point(center_x, center_y)
def grow_rectangle(self, x_offset, y_offset):
"""Modifies the Rectangle by adding to its width and height.
dwidth: change in width (can be negative).
dheight: change in height (can be negative).
"""
self.width += x_offset
self.height += y_offset
class Circle:
"""
Represents a circle in a 2D space.
:ivar center: The center of the circle as a Point object.
:type center: Point
:ivar radius: The radius of the circle.
:type radius: float
"""
def __init__(self, center, radius):
self.center = center
self.radius = radius
def is_point_inside(self, point):
"""
Determines if a point lies in or on the boundary of the circle.
:param point: The point to check.
:type point: Point
:return: True if the point lies in or on the boundary of the circle, False otherwise.
:rtype: bool
"""
return point.distance_to(self.center) <= self.radius
def rect_in_circle(circle, rectangle):
"""
Determines if a rectangle lies entirely in or on the boundary of a circle.
:param circle: The circle to check.
:type circle: Circle
:param rectangle: The rectangle to check.
:type rectangle: Rectangle
:return: True if the rectangle lies entirely in or on the boundary of the circle, False otherwise.
:rtype: bool
"""
# Get all four corners of the rectangle
bottom_left, bottom_right, top_left, top_right = rectangle.get_points()
# All corners must be in or on the circle
return (circle.is_point_inside(bottom_left) and
circle.is_point_inside(bottom_right) and
circle.is_point_inside(top_left) and
circle.is_point_inside(top_right))
################################################################################
def test_circle_creation():
# Test creating a circle
center = Point(150, 100)
radius = 75
circle = Circle(center, radius)
assert circle.center.x == 150
assert circle.center.y == 100
assert circle.radius == 75
print("Circle creation test passed!")
def test_point_in_circle():
# Test point_in_circle function
center = Point(150, 100)
radius = 75
circle = Circle(center, radius)
# Point inside the circle
point_inside = Point(160, 110)
assert circle.is_point_inside(point_inside) == True
# Point on the boundary of the circle
point_on_boundary = Point(150, 175) # (150, 100) + (0, 75)
assert circle.is_point_inside(point_on_boundary) == True
# Point outside the circle
point_outside = Point(300, 300)
assert circle.is_point_inside(point_outside) == False
print("Point in circle test passed!")
def test_rect_in_circle():
# Test rect_in_circle function
center = Point(150, 100)
radius = 75
circle = Circle(center, radius)
# Rectangle entirely inside the circle
rect_inside = Rectangle(50, 50, Point(125, 75))
assert rect_in_circle(circle, rect_inside) == True
# Rectangle partially inside the circle
rect_partial = Rectangle(100, 100, Point(125, 75))
assert rect_in_circle(circle, rect_partial) == False
# Rectangle entirely outside the circle
rect_outside = Rectangle(50, 50, Point(250, 250))
assert rect_in_circle(circle, rect_outside) == False
print("Rectangle in circle test passed!")
if __name__ == "__main__":
test_circle_creation()
test_point_in_circle()
test_rect_in_circle()
print("All tests passed!")
Circle creation test passed!
Point in circle test passed!
Rectangle in circle test passed!
All tests passed!
Exercise 15.2
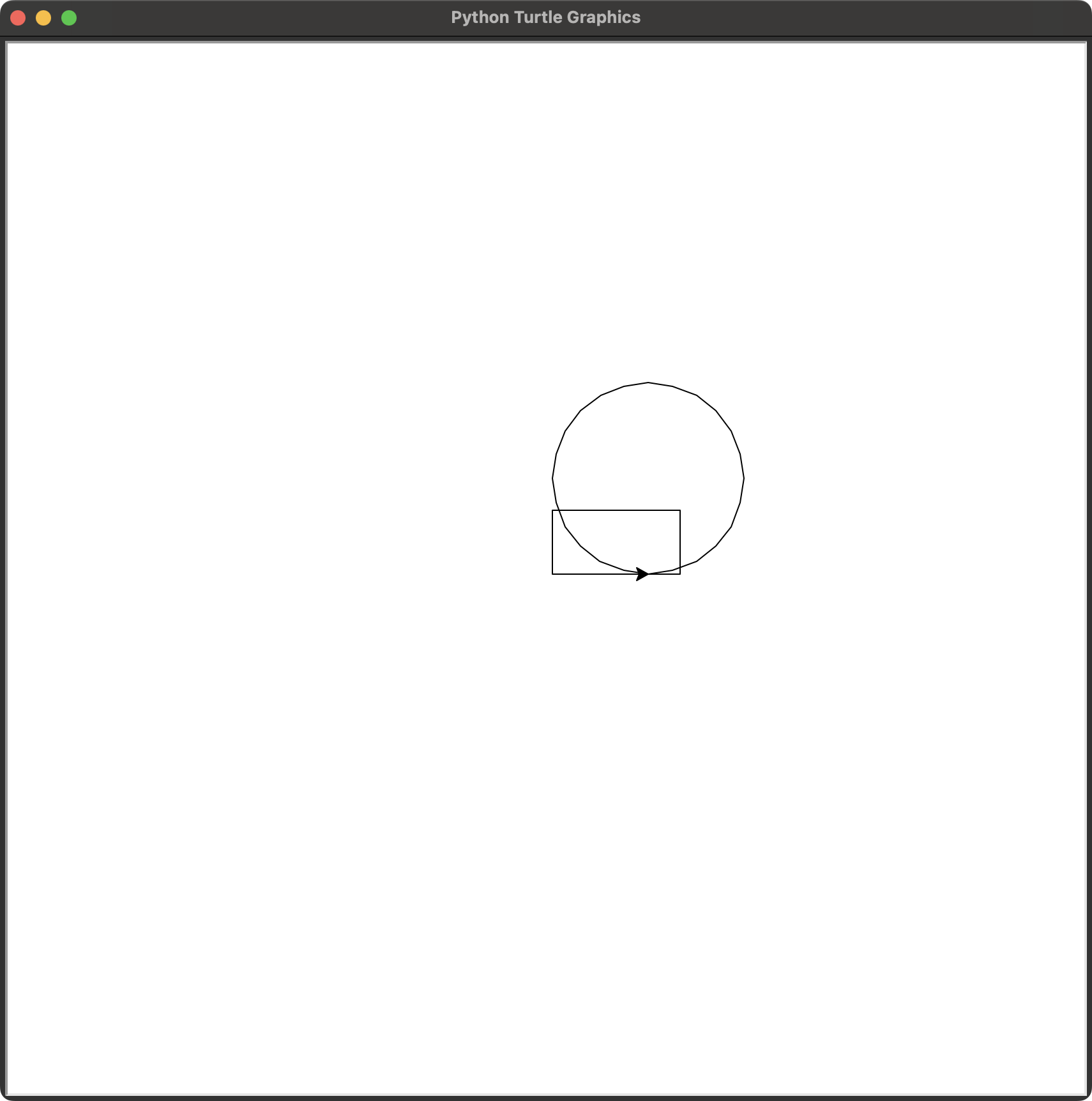
Write a function called draw_rect that takes a Turtle object and a Rectangle and uses the Turtle to draw the Rectangle. See Chapter 4 for examples using Turtle objects.
Write a function called draw_circle that takes a Turtle and a Circle and draws the Circle.
import turtle
from unit_1_1 import Point, Rectangle, Circle
def draw_rect(t, rect):
"""
Uses a Turtle object to draw a Rectangle.
:param t: The Turtle object to use for drawing.
:type t: turtle.Turtle
:param rect: The Rectangle to draw.
:type rect: Rectangle
"""
# Save the current pen state
pen_was_down = t.isdown()
# Get the four corners of the rectangle
bottom_left, bottom_right, top_left, top_right = rect.get_points()
# Move to the bottom-left corner without drawing
t.penup()
t.goto(bottom_left.x, bottom_left.y)
t.pendown()
# Draw the rectangle
t.goto(bottom_right.x, bottom_right.y) # Bottom edge
t.goto(top_right.x, top_right.y) # Right edge
t.goto(top_left.x, top_left.y) # Top edge
t.goto(bottom_left.x, bottom_left.y) # Left edge
# Restore the original pen state
if not pen_was_down:
t.penup()
def draw_circle(t, circle):
"""
Uses a Turtle object to draw a Circle.
:param t: The Turtle object to use for drawing.
:type t: turtle.Turtle
:param circle: The Circle to draw.
:type circle: Circle
"""
# Save the current pen state
pen_was_down = t.isdown()
# Move to the rightmost point of the circle without drawing
t.penup()
t.goto(circle.center.x + circle.radius, circle.center.y)
t.pendown()
# Draw the circle
t.circle(circle.radius)
# Restore the original pen state
if not pen_was_down:
t.penup()
if __name__ == "__main__":
# Create a turtle
t = turtle.Turtle()
t.speed(0) # Fastest speed
# Create a rectangle
rect = Rectangle(100, 50, Point(0, 0))
# Create a circle
circle = Circle(Point(0, 0), 75)
# Draw the rectangle
draw_rect(t, rect)
# Draw the circle
draw_circle(t, circle)
# Keep the window open
turtle.mainloop()
unit-1-2.py — Execution result